Graf 2

Graf Planar (Planar Graph) dan Graf Bidang (Plane Graph)

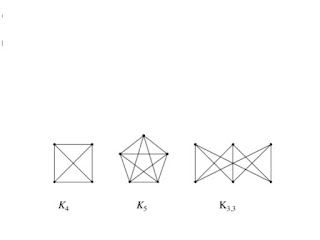
Graf yang dapat digambarkan pada bidang datar dengan sisi-sisi tidak saling memotong (bersilangan) disebut graf planar,  jika tidak, maka ia disebut graf tak-planar. K4 adalah graf planar:

Dan  K5 adalah graf tidak planar:

Graf planar yang digambarkan dengan sisi-sisi yang tidak saling berpotongan disebut graf bidang (plane graph).

Dan graf K(3,3) bukan graf planar

Aplikasi Graf Planar

• Perancangan IC (Integrated Circuit)

• Tidak boleh ada kawat-kawat di dalam ICboard yang saling bersilanganàdapat menimbulkan interferensi arus listrikàmalfunction

• Perancangan kawat memenuhi prinsip graf planar

 

Sisi-sisi pada graf bidang membagi bidang datar menjadi beberapa wilayah (region) atau muka (face).

Graf bidang pada gambar di bawah initerdiri atas 6 wilayah (termasuk wilayah terluar):

n – e + f = 2 (Rumus Euler) Pada Gambar di atas diketahui e = 11 dan n = 7, f = 6, n – e + f = 2 maka 7 – 11 + 6 = 2. Pada graf planar sederhana terhubung dengan f  buah wilayah, n buah simpul, dan e buah sisi (e > 2) selalu berlaku: e ≤ 3n – 6 Ketidaksamaan yang terakhir dinamakan ketidaksamaan Euler, yang dapat digunakan untuk menunjukkan keplanaran suatu graf sederhana,kalau graf planar, maka ia memenuhi ketidaksamaan Euler, sebaliknya jika tidak planar maka ketidaksamaan tersebut tidak dipenuhi. Contoh: Pada K4, n = 4, e = 6, memenuhi ketidaksamaan Euler, sebab 6 ≤ 3(4) – 6.  Jadi, K4 adalah graf planar. Pada graf K5, n = 5 dan e = 10, tidak memenuhi ketidaksamaan Euler  sebab 10 ≤ 3(5) – 6.  Jadi, K5 tidak planar Ketidaksamaan e ≤ 3n – 6 tidak berlaku untuk K3,3 karena   e = 9, n = 6   9 ≤ (3)(6) – 6 = 12 (jadi, e ≤ 3n – 6) padahal graf K3,3 bukan graf planar!  Buat asumsi baru: setiap daerah pada graf planar dibatasi oleh paling sedikit empat buah sisi,   Dari penurunan rumus diperoleh   e ≤ 2n – 4 Contoh Graf K3,3 pada Gambar di bawah memenuhi ketidaksamaan e ≤ 2n – 4, karena   e = 9, n = 6   9 ≤ (2)(6) – 4 = 8  (salah) yang berarti K3,3 bukan graf planar. Teorema Kuratoswki Berguna untuk menentukan dengan tegas keplanaran suatu graf. Gambar a.      Graf Kuratowski pertama (K5)      b.      Graf Kuratowski kedua (K3, 3)         c.       Graf yang isomorfik dengan graf Kuratowski kedua Sifat graf Kuratowski adalah: 1. Kedua graf Kuratowski adalah graf teratur. 2. Kedua graf Kuratowski adalah graf tidak-planar 3. Penghapusan sisi atau simpul dari graf Kuratowski menyebabkannya menjadi graf planar. 4. Graf Kuratowski pertama adalah graf tidak-planar dengan jumlah simpul minimum, dan   graf Kuratowski kedua adalah graf tidak-planar dengan jumlah sisi minimum. TEOREMA Kuratowski. Graf G bersifat planar jika dan hanya jika ia tidak mengandung upagraf yang isomorfik dengan salah satu graf Kuratowski atau homeomorfik (homeomorphic) dengan salah satu dari keduanya. Contoh: Kita gunakan Teorema Kuratowski untuk memeriksa keplanaran graf. Graf G di bawah ini bukan graf planar karena ia mengandung upagraf (G1) yang sama dengan K3,3. Graf G tidak planar karena ia mengandung upagraf yang sama dengan K3,3 Graf G tidak planar karena ia mengandung upagraf (G1) yang homeomorfik dengan K5 (dengan membuang simpul-simpul yang berderajat 2 dari G1, diperoleh K5).  Lintasan dan Sirkuit Euler Lintasan Euler ialah lintasan yang melalui masing-masing sisi di dalam graf tepat satu kali.   Sirkuit Euler ialah sirkuit yang melewati masing-masing sisi tepat satu kali..   Graf yang mempunyai sirkuit Euler disebut graf Euler (Eulerian graph). Graf yang mempunyai lintasan Euler dinamakan juga graf semi-Euler (semi-Eulerian graph). Contoh.  Lintasan Euler pada graf (a) : 3, 1, 2, 3, 4, 1 Lintasan Euler pada graf (b) : 1, 2, 4, 6, 2, 3, 6, 5, 1, 3 Sirkuit Euler pada graf (c)    : 1, 2, 3, 4, 7, 3, 5, 7, 6, 5, 2, 6, 1 Sirkuit Euler pada graf (d)    : a, c, f,  e, c, b, d, e, a, d, f, b, a Graf (e) dan (f) tidak mempunyai lintasan maupun sirkuit Euler Gambar : (a) dan (b) graf semi-Euler (c) dan (d) graf Euler (e) dan (f) bukan graf semi-Euler atau graf Euler TEOREMA. Graf tidak berarah memiliki lintasan Euler jika (graf semi-Euler) dan hanya jika terhubung dan memiliki dua buah simpul berderajat ganjil atau tidak ada simpul berderajat ganjil sama sekali.  TEOREMA. Graf tidak berarah G adalah graf Euler (memiliki sirkuit Euler) jika dan hanya jika setiap simpul berderajat genap. TEOREMA.  (a) Graf berarah G memiliki sirkuit Euler jika dan hanya jika G terhubung dan setiap simpul memiliki derajat-masuk dan derajat-keluar sama.  (b) G memiliki lintasan Euler jika dan hanya jika G terhubung dan setiap simpul memiliki derajat-masuk dan derajat-keluar sama kecuali dua simpul, yang pertama memiliki derajat-keluar satu lebih besar derajat-masuk, dan yang kedua memiliki derajat-masuk satu lebih besar dari derajat-keluar. Gambar   (a) Graf  berarah Euler (a, g, c, b, g, e, d, f, a)                  (b) Graf berarah semi-Euler (d, a, b, d, c, b)          (c) Graf berarah bukan Euler maupun semi-Euler Lintasan dan Sirkuit Hamilton Lintasan Hamilton ialah lintasan yang melalui tiap simpul di dalam graf tepat satu kali.   Sirkuit Hamilton ialah sirkuit yang melalui tiap simpul di dalam graf tepat satu kali, kecuali simpul asal (sekaligus simpul akhir) yang dilalui dua kali.  Graf yang memiliki sirkuit Hamilton dinamakan graf Hamilton, sedangkan graf yang hanya memiliki lintasan Hamilton disebut graf semi-Hamilton.  Gambar : (a) graf yang memiliki lintasan Hamilton (misal: 3, 2, 1, 4) (b) graf yang memiliki lintasan Hamilton (1, 2, 3, 4, 1) (c) graf yang tidak memiliki lintasan maupun sirkuit Hamilton TEOREMA.  Syarat cukup supaya graf sederhana G dengan n (≥ 3) buah simpul adalah graf Hamilton ialah bila derajat tiap simpul paling sedikit n/2 (yaitu, d(v) ≥ n/2 untuk setiap simpul v di  G).  (coba nyatakan dalam “jika p maka q”)  TEOREMA.  Setiap graf lengkap adalah graf Hamilton. TEOREMA. Di dalam graf lengkap G dengan n buah simpul (n ≥ 3), terdapat (n – 1)/2 buah sirkuit Hamilton. TEOREMA. Di dalam graf lengkap G dengan n buah simpul (n ≥ 3 dan n ganjil), terdapat (n – 1)/2 buah sirkuit Hamilton yang saling lepas (tidak ada sisi yang beririsan). Jika n genap dan n  ≥ 4, maka di dalam G terdapat (n – 2)/2 buah sirkuit Hamilton yang saling lepas. Beberapa graf dapat mengandung sirkuit Euler dan sirkuit Hamilton sekaligus, mengandung sirkuit Euler tetapi tidak mengandung sirkuit Hamilton, dan sebagainya. Gambar: (a) Graf Hamilton sekaligus graf Euler   (b) Graf Hamilton sekaligus graf semi-Euler Beberapa Aplikasi Graf ·         Lintasan terpendek (shortest path) (akan dibahas pada kuliah IF3051) ·         Persoalan pedagang keliling (travelling salesperson problem) ·         Persoalan tukang pos Cina (chinese postman problem) ·         Pewarnaan graf (graph colouring)

Hubungan antara jumlah simpul (n), jumlah sisi (e), dan jumlah wilayah (f) pada graf bidang: